Minimalflächen
Minimalflächen lassen sich experimentell durch Seifenhäute erzeugen. Taucht man eine irgendwie geformte Drahtschlinge in eine Seifenlösung, so bildet sich in der Schlinge bei vorsichtigem Herausziehen ein hauchfeiner Film. Wegen seiner Oberflächenspannung nimmt das Seifenhäutchen eine Form an, in der seine potentielle Energie minimal ist. Da diese Energie proportional zum Flächeninhalt ist, hat die Seifenhaut einen kleineren Flächeninhalt als jede andere noch so geringfügig geformte Fläche, die in dieser Drahtschlinge eingespannt ist. Mathematisch sind Minimalflächen, Flächen, deren mittlere Krümmung in allen Punkten Null ist. D.h. bei Minimalflächen sind die Krümmungen der beiden maximalen Normalschnitte gleich groß. Dieses Gleichgewicht der Krümmungen ist mit ein Grund für den ästhetischen Reiz von Minimalflächen.
Man kann zeigen, daß sich nicht-konstante Minimalflächen sich durch den folgenden Satz an Integralen
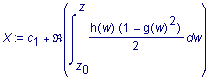
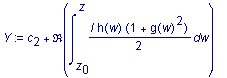
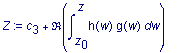
(sog. Weierstrass-Darstellung) konstruieren lassen. Hierin sind g(z) und h(z) holomorphe Funktionen über einer einfach zusammenhängenden Domäne.
In MAPLE V haben diese Abbildungen die Gestalt (mit der Annahme f(z)=h(z)/2,g(z)=z)
X:=unapply(Re(subs(z=r*exp(I*phi),int(f(zeta)*(1-zeta^2),zeta=1..z))),r,phi);
Y:=unapply(Re(subs(z=r*exp(I*phi),int(I*f(zeta)*(1+zeta^2),zeta=1..z))),r,phi)
Z:=unapply(Re(subs(z=r*exp(I*phi),int(2*zeta*f(zeta),zeta=1..z))),r,phi);
plot3d([X(r,phi),Y(r,phi),Z(r,phi)],r=r_min..r_max,phi=phi_min..phi_max);
Verschiedene Beispiele für
Minimalflächen, die auf diese Weise mit MAPLE V erzeugt
wurden sind auf dieser Seite
dargestellt.
Komplexere Minimalflächen
hingegen lassen
sich mit MAPLE nur mit sehr hohen Computer-Aufwand
(CPU-Zeit, Memory) generieren. Eine Möglichkeit
komplexere Flächen zu rendern bietet POV (Persistence
of Vision Ray Tracer). Das Rendering Modell von POV beruht
auf dem "Phong shading" Modell. In diesem Modell werden die
Normalen-Vektoren der darzustellenden Flächen in
signifikanter Weise benutzt. POV erwartet Flächendaten
in dem Format:
smooth_triangle {
<p11 p12 p13>, <n11 n12 n13>
<p21 p22 p23>, <n21 n22 n23>
<p31 p32 p33>, <n31 n32 n33>
}
Darin sind (p11 p12 p13),(p21 p22 p23),(p31 p32 p33) die Eckpunkte eines Flächen-Dreiecks welches die darzustellende Fläche approximieren und (n11 n12 n13),(n21 n22 n23),(n31 n32 n33) die Koordinaten der Normalenvektoren an diesen Punkten. Ausgehend von der Weierstrass-Darstellung für Minimal-Flächen (s.o.) und den Weierstrass-Daten g(z), h(z) lassen sich diese Koordinaten mit MAPLE auf die folgende Weise erzeugen:
X:=unapply(Re(subs(z=r*exp(I*phi),int(h(z)/2*(1/g(z)-g(z)),z))),r,phi)
Y:=unapply(Re(subs(z=r*exp(I*phi),int(I*h(z)/2*(1/g(z)+g(z)),z))),r,phi)
Z:=unapply(Re(subs(z=r*exp(I*phi),int(h(z),z))),r,phi);;
norm:=unapply(abs(g(z)^2)+1,z);
nX:=unapply(2*Re(subs(z=r*exp(I*phi),(2*Re(g(z))/norm(z)))),r,phi)
nY:=unapply(2*Im(subs(z=r*exp(I*phi),(2*Im(g(z))/norm(z)))),r,phi)
nZ:=unapply(subs(z=r*exp(I*phi),(abs(g(z)^2)-1)/norm(z)),r,phi);
s:="data.inc";
dr:=(r_max-r_min)/n;
dphi:=(phi_max-phi_min)/m;
mtopov2:=proc(n,m,umin,du,vmin,dv,s)
local i, j, u1, u2, v1, v2, x1, x2, x3, x4, y1, y2, y3, y4,
z1, z2, z3, z4, nx1, nx2, nx3, nx4, ny1, ny2, ny3, ny4, nz1,
nz2, nz3, nz4;
for i from 1 by 1 to n do
u1:=umin+(i-1)*du:
u2:=umin+i*du:
for j from 1 by 1 to m do
v1:=vmin+(j-1)*dv:
v2:=vmin+j*dv:
x1:=evalf(X(u1,v1)):y1:=evalf(Y(u1,v1)):z1:=evalf(Z(u1,v1)):
x2:=evalf(X(u2,v1)):y2:=evalf(Y(u2,v1)):z2:=evalf(Z(u2,v1)):
x3:=evalf(X(u2,v2)):y3:=evalf(Y(u2,v2)):z3:=evalf(Z(u2,v2)):
x4:=evalf(X(u1,v2)):y4:=evalf(Y(u1,v2)):z4:=evalf(Z(u1,v2)):
nx1:=evalf(nX(u1,v1)):ny1:=evalf(nY(u1,v1)):nz1:=evalf(nZ(u1,v1)):
nx2:=evalf(nX(u2,v1)):ny2:=evalf(nY(u2,v1)):nz2:=evalf(nZ(u2,v1)):
nx3:=evalf(nX(u2,v2)):ny3:=evalf(nY(u2,v2)):nz3:=evalf(nZ(u2,v2)):
nx4:=evalf(nX(u1,v2)):ny4:=evalf(nY(u1,v2)):nz4:=evalf(nZ(u1,v2)):
fprintf(s,`%s\n %c %g %c %g %c %g %s %g %c %g %c %g %s\n %c
%g %c %g
%c %g %s %g %c %g %c %g %s\n %c %g %c %g %c %g %s %g %c %g
%c %g %s\n`,
`smooth_triangle{`,
`<`,x1,`,`,y1,`,`,z1,`>,<`,nx1,`,`,ny1,`,`,nz1,`>,`,
`<`,x2,`,`,y2,`,`,z2,`>,<`,nx2,`,`,ny2,`,`,nz2,`>,`,
`<`,x3,`,`,y3,`,`,z3,`>,<`,nx3,`,`,ny3,`,`,nz3,`>}`);
fprintf(s,`%s\n %c %g %c %g %c %g %s %g %c %g %c %g %s\n %c
%g %c %g
%c %g %s %g %c %g %c %g %s\n %c %g %c %g %c %g %s %g %c %g
%c %g %s\n`,
`smooth_triangle{`,
`<`,x1,`,`,y1,`,`,z1,`>,<`,nx1,`,`,ny1,`,`,nz1,`>,`,
`<`,x3,`,`,y3,`,`,z3,`>,<`,nx3,`,`,ny3,`,`,nz3,`>,`,
`<`,x4,`,`,y4,`,`,z4,`>,<`,nx4,`,`,ny4,`,`,nz4,`>}`);
od:
od:
fclose(s):
end:
mtopov2(n,m,r_min,dr,phi_min,dphi,s);